|
Wavelet collocation method to solve partial differential equations |
李镐俊 (Karlsruhe) |
|
|
Conditional Random Field and its applications |
王克宇 (Göttingen) |
|
|
关于Birch和Swinnerton-Dyer猜想 |
赵经纬 (Karlsruhe) |
|
|
Lattice Boltzmann methods and asymptotic analysis |
Dr. Yang, Zhaoxia (Konstanz) |
|
|
Solutions to viscous model of quantum hydrodynamics |
刘庆喆 (Konstanz) |
|
|
电影: Julia Robinson and Hilbert’s Tenth Problem |
|
|
|
Quantitative Methods in High-Frequency Financial Econometrics: Modeling Univariate and Multivariate Time Series |
Dr. 孙玮 (Karlsruhe) |
|
|
PET和肿瘤的精确放射治疗 |
施匡宇 (München) |
|
|
Mathematik und Banken |
周晗 (Frankfurt a. M.) |
|
|
Clifford Algebra简介 |
张耀坤 (Karlsruhe) |
|
|
电影: 二维电影(Flatland) |
|
[9:10-9:40]
李镐俊
Karlsruhe大学数学系
haojun.li@math.uni-karlsruhe.de
We introduce how to use WCM(wavelet collocation method) to solve partial differential equations, and we compare it with traditional computational method-FDM(finite difference method), then, 2D structured Maxwell's equations are solved with both of two methods as a numerical example for our discussion.
Conditional Random Field and its applications
[9:40-10:20]
王克宇
Göttingen大学理论信息系
Keyu.Wang@informatik.uni-goettingen.de
本报告主要介绍一个概率模型CRF。这个模型主要应用在统计分类领域。在这个报告里,我首先简单介绍一下这个模型,然后举出一个成功的应用,最后谈一谈我的研究项目,如何将CRF应用到生物信息领域。
[10:20-11:10]
赵经纬
Karlsruhe大学数学系
本报告主要围绕美国Clay数学研究所于2000年宣布的七个千禧数学难题之一的Birch和Swinnerton-Dyer猜想以及Coates, Wiles于1978年对此猜想在特殊条件下的证明。首先介绍椭圆曲线的定义和主要性质,以及椭圆曲线的复乘,Hasse-Weil-Zeta函数,Idel群的特征标,有复乘的椭圆曲线的L函数,然后给出BSD猜想的具体内容。对Coates和Wiles在证明中主要用到的一些数学工具例如形式群理论,类域论和椭圆单位元也将做一定介绍。最后概括性描述CW证明的大体步骤。
Lattice Boltzmann methods and asymptotic analysis
[11:20-11:55]
Dr. Yang, Zhaoxia
Fachbereich Mathematik und Statistik, Universität Konstanz
In this talk, the background of the mesoscopic lattice Boltzmann methods is first introduced. The lattice Boltzmann methods are mainly used to simulate the macroscopic imcompressible fluid dynamics govened by the Navier-Stokes equation. In fact, this kind of methods can be viewed as finite difference schemes in the mathematical view. The asymtotic analysis is then applied to reveal explicitly the connection between mesoscopic lattice Boltzmann methods and macroscopic Navier-Sokes equations and to carry out their numerical analysis: accuracy, stability and convergence.
Solutions to viscous model of quantum hydrodynamics
[11:55-12:45]
刘庆喆
Fachbereich Mathematik und Statistik, Universität Konstanz
There are several different models simulating the flow of charged particles. For example, quantum energy transport models, the quantum drift diffusion model,the quantum hydrodynamic model(QHD). In this paper we study the viscous QHD model which is derived from the Wigner equation with the Fokker-Planck collision operator:
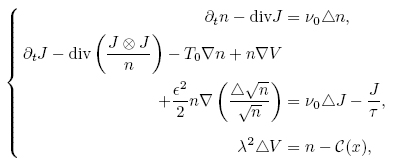
The unknown functions are n, J, V which model the particle density, the current density and the electrostatic potential respectively.
Until now several results only for special cases are derived. M. Dreher and L. Chen proved the existence of local-in-time solutions on a torus in 2007, it seems that the viscous model of QHD in higher dimensions has been analytically investigated for the first time at that time. In 2008 M. Dreher checked that the corresponding matrix operator concerning the spatial variables is of mixed order in the sense of Douglis and Nirenberg(1959), and approximated the system by introducing a fourth order viscous regularization. In this paper we first investigate the matrix operator deeply to give a detailed proof to obtain a better property of this operator that it is elliptic with parameter in some sector with vertex at the origin in the sense of Fairman(2006). From this the a priori estimates can be derived. Second we solve the corresponding linear system without introducing a viscous regularization term. Then study the original system by compactness arguments and iteration method. More precisely, we first shrink the time interval to ensure some boundedness assumptions, second derive uniform bounds of the approximated solutions, third prove that the time interval can not tend to zero, finally use contraction mapping to infer the uniqueness of weak limits. The limit is expected to be the local-in-time solution. Furthermore we investigate the global extension on a torus and the exponential stability to a stationary state.
[15:05-15:45]
Dr. 孙玮
Institute of Statistics and Mathematical Economics,
University of Karlsruhe, Germany
wei.sun@statistik.uni-karlsruhe.de
This thesis establishes an entire theoretical framework for high frequency financial econometrics. The major innovations of this thesis are: (1) introduce a new volatility model, i.e., the ARMA-GARCH-fractional stable model, to capture the stylised facts, such as volatility clustering, heavy tailedness, and long-range dependence, observed from the data; (2) improve the ACD model by employing fractional stable noise and stable distribution; (3) propose a bootstrapping test for goodness-of-fit evaluation; (4) introduce a new multivariate time series model, i.e., the ARMA-GARCH-fractional stable model with “t”-copula for analysing interrelationship between international equity markets when those markets exhibit symmetric correlation; and (5) introduce a new model, i.e., the ARMA-GARCH-fractional stable model with skewed “t”-copula for analysing multivariate time series when these series illustrate asymmetric correlation. The results of empirical studies show the superior performance of these models in analysing high-frequency financial data comparing to the models based on classical assumption of normal distribution and extreme value distributions.
[15:45-16:15]
施匡宇
Klinikum rechts der Isar, Technische Universitaet Muenchen
本报告将讨论PET医学影像以及以此为基础的肿瘤的精确放射治疗,重点挖掘数学原理在这些技术中的运用。首先我们将介绍PET的基本原理以及其基本三维重建算 法。随后我们会讨论PET影像的处理,尤其是在此基础上的肿瘤识别和分割。最后我们将探讨由次结合生物病理学原理带来现代放射治疗技术的一些新的理念。
[16:25-16:55]
周晗
Global Markets -Transaction Management Group, Deutsche Bank AG
Eine Einfürung über erste Anwendung der Mathematik wird ausgeführt.
1) Eine Überblick des Einsatz der Mathematik in Banking: a) Mathematik in Risiko Controlling; b) Mathematik in Aktienhandel; c) Mathematik in Rates Produkte.
2) Turbo-Optionscheinen und einfache Statistik (Anwendung in Risk Controlling): Am Anfang des Jahres war der Aktienmarkt volatil. Vielen Banken emittieren Turbo-Optionscheine. Wie erhielt der Banker eine Übersicht über das eingehende Risiko? Einfache statistischen Modelle hilft dabei die Problematik zu lösen.
[16:55-17:25]
张耀坤
卡尔斯鲁厄大学计算机系
Clifford Algebra通过定义一种新的乘法运算Geometric Product及适当的坐标系选取,将各种几何运算简化为若干Multivector的Geometric Product,代替了矩阵运算,从而简化了运算及提高了数值稳定性。在机器人学及计算机视觉中有着越来越广泛的应用。
报告提纲:
1. 几何代数(Geometric Algebra)定义及基本性质
2. 空间旋转及平移的几何代数表示(Rotor & Motor Algebra)
3. G410代数(Conformal Geometry)及应用实例
电影: Julia Robinson and Hilbert’s Tenth Problem
[14:00-14:55]
A one-hour biographical documentary, Julia Robinson and Hilbert's Tenth Problem tells the story of an important American mathematician against a background of mathematical ideas.
Julia Robinson, a pioneer among American women in mathematics, rose to prominence in a field where often she was the only woman. Julia Robinson was the first woman elected to the mathematical section of the National Academy of Sciences, and the first woman to become president of the American Mathematical Society. Her work, and the exciting story of the path that led to the solution of Hilbert's tenth problem in 1970, produced an unusual friendship between Russian and American colleagues at the height of the cold war. In this film, Robinson's major contribution to the solution of H10 triggers a tour of 20th century mathematics that moves from Paris in 1900, through the United States, to the Soviet Union and back. Following the passionate pursuit of an unsolved problem by several individuals in different countries adds to the emotional intensity of the mathematical quest.
The film covers important events in the history of modern mathematics while conveying the motivations of mathematicians, and exploring the relationship between mathematical research and the development of computers. The key protagonists and advisors to the project are recognized as the most prominent in their fields.
Julia Robinson's story, and the presence of prominent women in mathematics in the film, should inspire young women to pursue educational opportunities and careers in mathematics.
[17:25-18:00]
电影Flatland是由1884年一位英国牧师Edwin A. Abbott(1838-1926)所撰写的一本小册子《Flatland》改编的一部动画片。小说里构造了一个全新的世界──这个世界是二维的!整个小说分成两个部分,前一部分系统地描述这个二维世界,包括自然状况、居民生活、政治历史等等。真正有趣的事情发生在后一部分里,这里不同维度的世界之间发生了碰撞——二维世界中的主人公拜访了一维世界,同时又接触到了一个全新的三维世界。当他在他的世界传播三维思想时,整个世界大乱,哥白尼时代的那段故事再次发生。2007年的片子,英文版,片长34分钟 。